在关于定向穿越扩孔钻进的研究中，楼岱莹等都只对扩孔后孔眼孔形进行了定性的说明，并没有对其进行定量的分析，并且在穿越工程中孔眼周围的岩土力学行为的研究中，几乎所有的研究者都是针对圆形孔眼进行的解析法、数值法和实验法分析，没有结合工程中孔眼为椭圆形的现状。对扩孔形状的研究，有利于孔形的控制和优化，为工程施工及后续研究提供理论依据。

本文采用数值模拟方法，对扩孔过程进行了有限元分析 ，通过与现有单齿正交切削岩土的三维力学计算模型进行对比，验证了该有限元模型的准确性与可靠性，zui后，运用该模型进行了不同工况下扩孔器沉降量的规律预测分析。

1.扩孔理论模型

在回拖扩孔过程中，扩孔器对岩土的切削性能对扩孔效率有很大的影响，图 1 为扩孔器工作时的受力简图，在分析扩孔钻进时岩土切削的力学特性时，贾彦杰等 综合考虑岩土与切削齿面之间的接触摩擦及岩土剪切区的剪切作用，推导了不同岩土材料下单齿正交切削岩土的解析解。

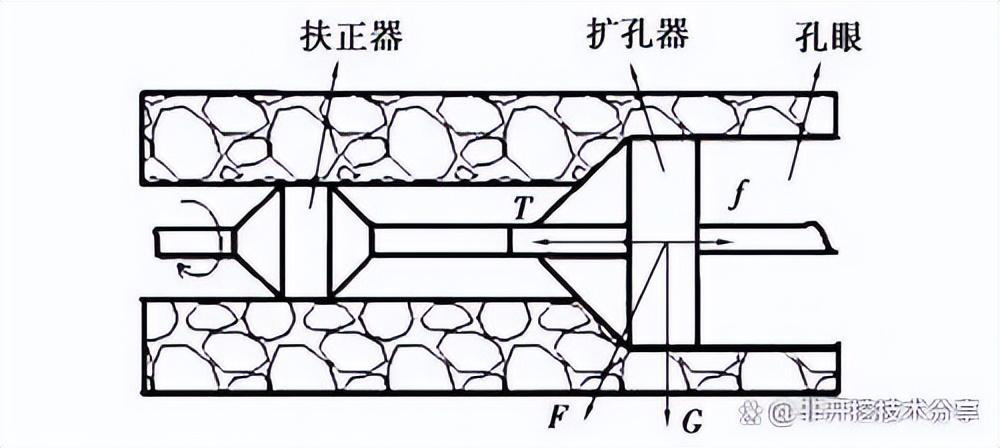
图 1 扩孔器—岩土系统简图

如图 2 所示为单齿正交切削时的剪切平面。岩屑部分与切削齿面的接触面受到的正压力 F→nf 和摩擦力 F→f 的作用，其合力为 F→rf ，剪切平面上有正压力 F→ns 和剪切力 F→s ，其合力为 F→rs ; φ 为被切削岩土材料的剪切角。

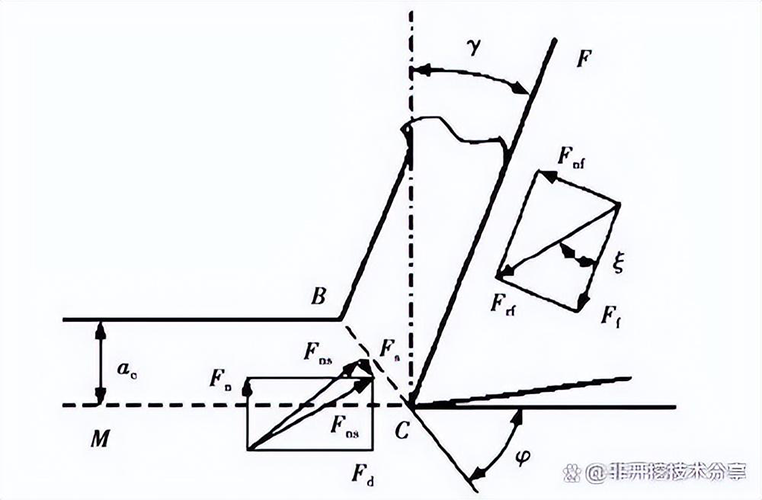
图 2 剪切平面

根据 静 力 平 衡 和 岩 土 材 料 修 正 的 线 性Drucker-Prager 模型可以得到剪切平面上的剪切力，有:

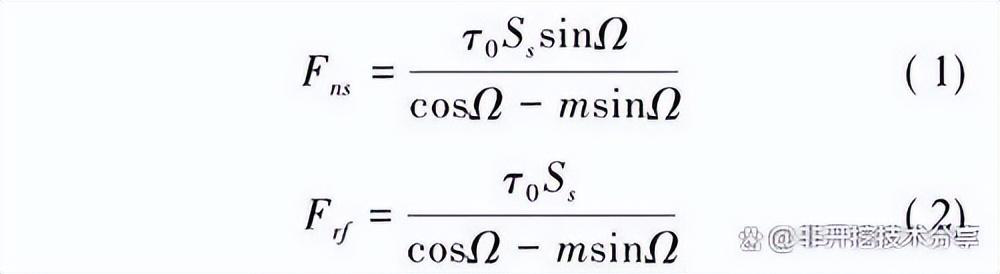
式中: S s 为剪切平面的面积，Ω = γ + φ + ξ，其中，φ 为被切削岩土材料的剪切角，γ 为切削齿的齿前角; ξ为岩土切削与单齿切削表面之间的摩擦角; m =－ 槡 6α，α 是与岩土材料粘聚力和内摩擦角相关的参数。

将切削齿上的合力 F→rf 向切削速度方向和切削平面的法向方向投影，得到的分力分别为切削力F→d 和切削平面的法向力 F→n :

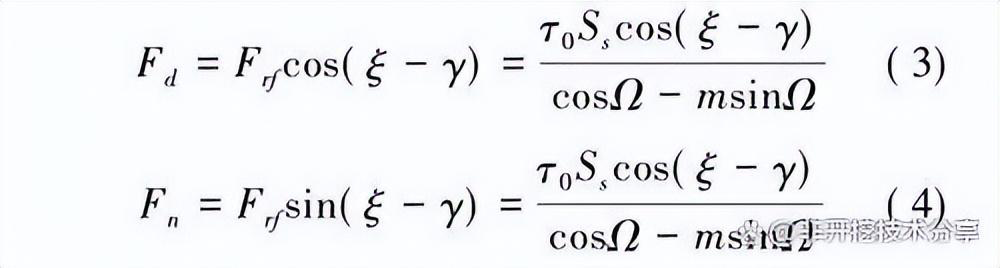
2.数值模拟和验证

2．1 岩土-扩孔器模型

在岩土模型中，上一级的孔眼半径为0.46m，扩孔半径为0.53m。为了消除模型尺寸和回拖时孔形状对应力分布产生的影响，选取孔壁上下左右尺寸分别为回拖孔半径的 6 倍，故岩土模型横切面长、宽均为3.4m，纵向长度为15m。扩孔器与地层均采用显式 3D 应力缩减积分单元，该单元在求解地层岩土失效与岩土去除等高度非线性问题上优势明显 。为减小计算量，孔眼附近进行网格加密。

图 3 岩土模型

常见的扩孔器有翼状扩孔钻头、螺旋形扩孔钻头、凹槽状扩孔器、牙轮式扩孔钻头、环刀型扩孔钻头、双向纺锤型扩孔钻头和粗径钻具型扩孔钻头。因为翼状扩孔钻头的旋转阻力低，扩孔速度快，保直能力好，适用于较硬土层 ，故本文对翼状扩孔钻头中的板桶式扩孔钻头进行建模。扩孔器的zui大外径为需扩孔眼直径，为1.06m，如图 4 所示为板桶式扩孔钻头模型。对于扩孔器上的切削齿，由于穿越深度一般在 0～100 m 之间 ，穿越的深度非常浅，而工程施工中所遇岩土多为粉黏土或粉土，基本是新生代第四纪形成的地层，相对于这些岩土层而言扩孔器的硬度很大，故将扩孔器钻头处理成刚体，扩孔器前端为钻杆。

图 4 扩孔器模型

2．2 材料定义

岩土层材料本构采用Drucker-Prager 模型。岩土的参数如表 1 和表 2 所示。将扩孔器与钻杆的材料等效为钢，其密度为 7800 kg/m3 。切削齿的弹性模量为 210 GPa，泊松比为0.3 。表 3 为扩孔器切削齿的参数。

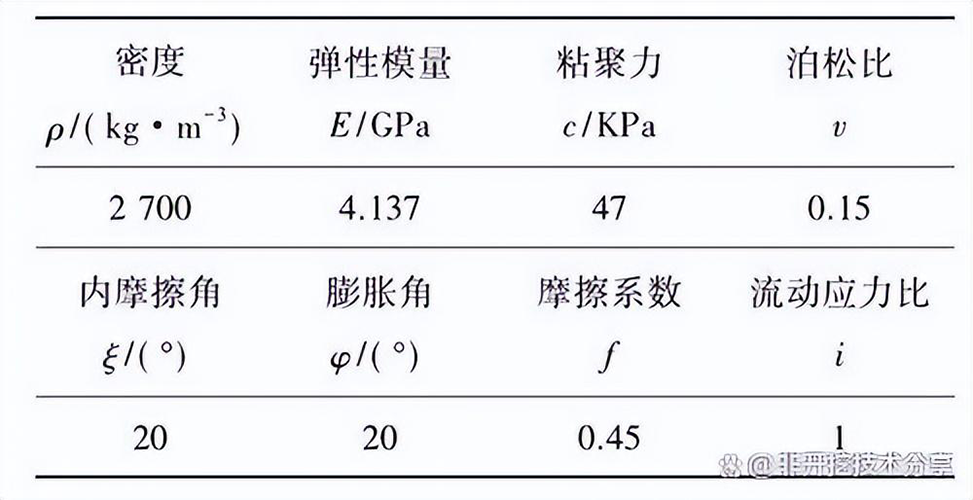
表 1 岩土参数表

表 2D-P 模型硬化参数

表 3 切削齿的参数

2．3 载荷与边界条件

2.3.1 分析步

Step1: 模拟扩孔器初始状态和岩土初始地应力分布。对扩孔器和钻杆施加重力加速度 9.8m/s2 ，模拟扩孔器和钻杆的自重; 对岩土模型的前表面施加水平侧压2.5MPa，上表面施加方土体压力1.65MPa，模拟岩土初始地应力。

Step2: 分析扩孔器钻进速度和自转速度对孔形下沉量的影响。岩土的初始地应力与扩2.3.2 接触和边界条件

扩孔器前后连接钻杆，钻杆与扩孔器之间属于螺纹连接，钻杆的后端面与扩孔器的前端面位移保持一致，在扩孔器前端面上设置参考点，将钻杆后端面与该参考点耦合。为了减少运算量，采用边界约束的作用代替扶正器效果，因此，本模型中将扶正器简化为 X、Y 两个方向的位移约束。

岩土模型的底面设为固定约束，岩土模型的上表面和两侧面为自由表面，默认模型分析初始状为扩孔器已经进入孔内完成了部分扩孔，因此岩土内部尺寸右边为已扩直径，左边为上一级扩孔直径。图 5 为扩孔器岩土的网格剖面模型。

对扩孔器和孔壁之间设置面面接触，切削齿的外表面为主接触面，在扩孔作用下将发生变形的土体为从接触面，并设定扩孔器和岩土之间的滑动摩擦系数为0.2。

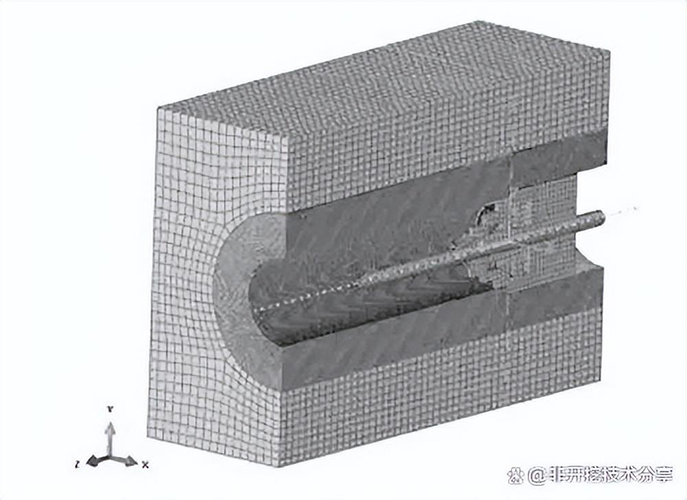
图 5 扩孔器-岩土网格模型

2．4 数值模拟结果验证

为了模拟单齿正交切削状态，将扩孔器的旋转速度设为 ω =0 rad/s，当钻进速度 v=0.01m/s 时，扩孔器前进过程中的地层应力变化云图如图 6 所示，在 此 时 扩 孔 器 进 入 地 层 的 zui大 应 力 为31.72 MPa。对于切削齿切下的岩土碎片，预先设定失效准则的临界值，当材料退化到临界值时，软件则判断该单元已经失效，自动删除失效单元。在切削过程中，岩土单元由弹性阶段经塑性阶段到损伤阶段的变化过程中，切削齿会受到变载荷的作用，图 7 即为齿前角为 0°时候的切削齿上主切削力随时间的变化曲线和理论三维模型下的主切削力对比图。由图可以看出，仿真中的主切削力处于波动状态，其平均值为173 N，与理论解的186 N 非常接近，相差仅为 7%。这说明本岩土模型在一定程度上具有较高的可靠性。

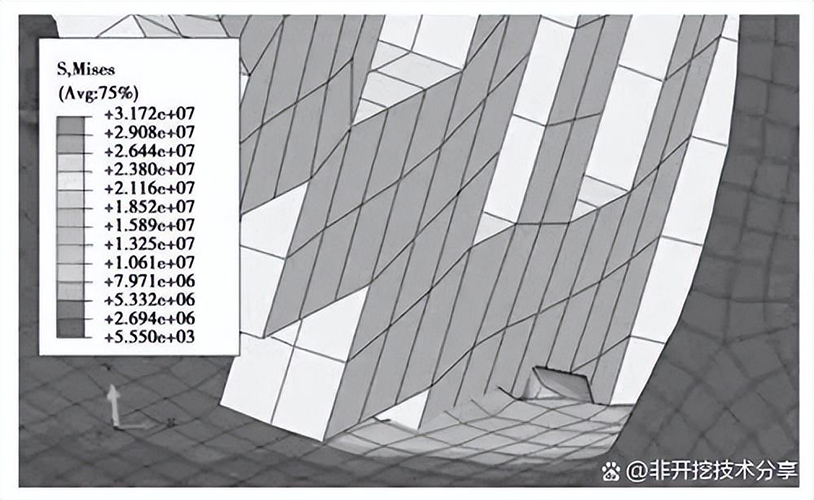
图 6 扩孔器切削时岩土的应力云图

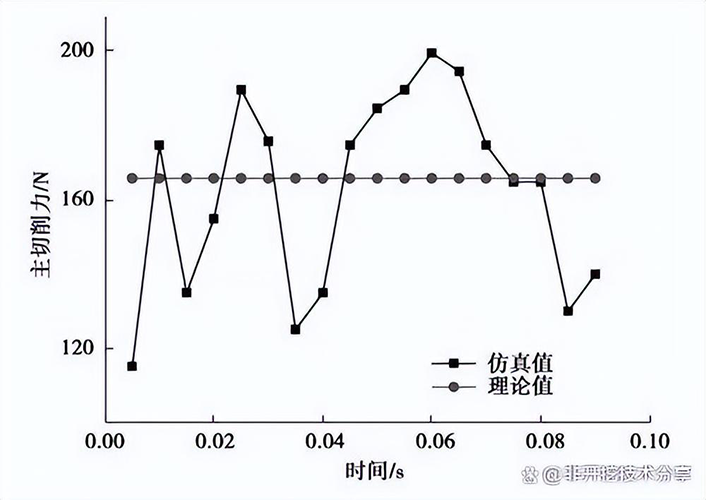
图 7 仿真结果与理论值对比图

3.孔形偏移影响规律分析

3．1 孔眼横向偏移和纵向偏移

当扩孔器钻速 v = 0.01m/s、旋转速度为 ω =3 rad/s 时，如图 8 所示为扩孔器扩孔过程中钻头的纵向偏移和横向偏移随着扩孔器钻进位移变化出现的情况。扩孔过程中扩孔器与地层接触不连续，产生振动的同时，将会出现钻进中心偏移。由图 8 可以看出，zui大纵向偏移距离达到了0.013m，也即是扩孔器下沉了0.013 m，扩孔器的zui大横向位移达到了0.009 m。

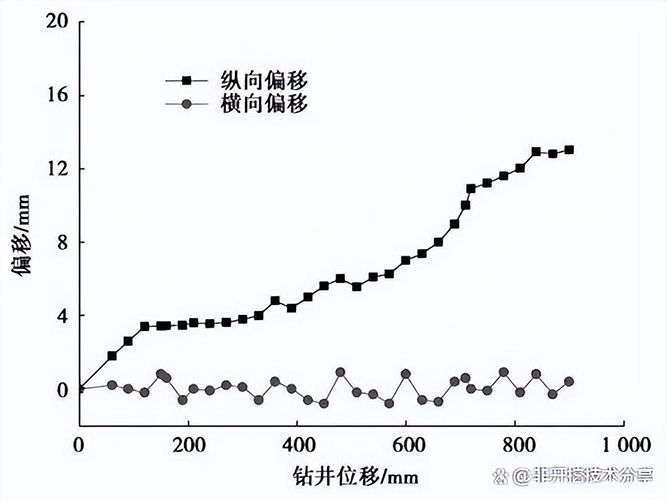
图 8 横向与纵向位移-钻进位移曲线

3．2 扩孔器钻速和钻进速度对孔眼偏移的规律

(1) 为了得到钻头钻进速度对扩孔器下沉量的影响，在数值模拟的工况中，将扩孔器旋转速度固定为 ω =3 rad/s，通过改变扩孔器的钻进速度得到钻进速度与下沉量之间的关系。钻进速度分别取为 4 mm/s，6 mm/s，8 mm/s，10 mm/s，12 mm/s。不同钻速下的沉降量曲线图如图 9 所示。

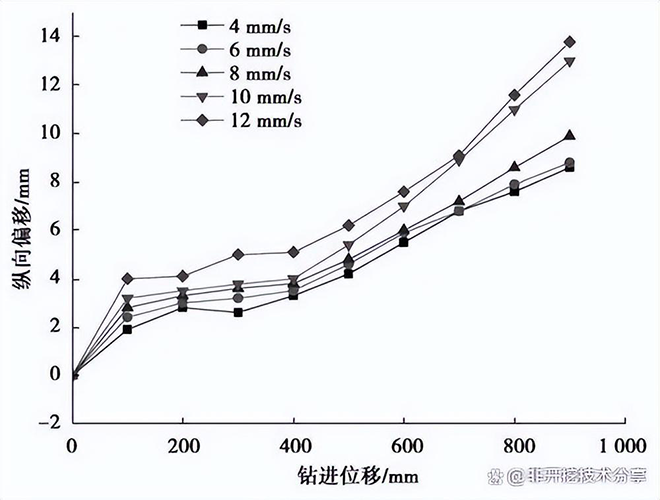
图 9 不同钻进速度下扩孔器的下沉量

由图 9 看出，扩孔器钻进的速度越大，扩孔器振动的频率越高，增加了单位时间对穿越地层的切削作用，纵向位移将增大，扩孔器下沉量加剧。

(2) 为了得到钻头旋转速度对扩孔器下沉量的影响，在数值模拟的工况中，将扩孔器钻进速度固定为 ν = 10mm/s，通过改变扩孔器的旋转速度得到旋转速度与下沉量之间的关系，旋转速度分别取为 2 rad/s，2．5 rad/s，3 rad/s，3．5 rad/s，4 rad/s。不同旋转速度下的沉降量曲线图如图 10 所示。

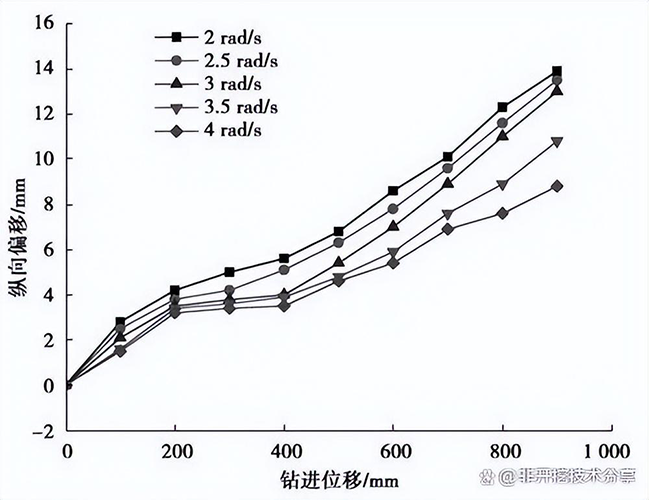
图 10 不同旋转速度下扩孔器的下沉量

由图 10 可以知道，扩孔器的旋转速度越大，孔眼在纵向上的位移越小，即在一定范围内提高扩孔器的旋转速度，有利于减小扩孔器的下沉量。

为了衡量扩孔器下沉量的大小，用单位位移沉降量的大小来表示下沉程度，图 11 即为不同钻进速度和不同旋转速度下，扩孔器在单位位移上的下沉量趋势图。由图 11 可以看出，单位位移上的沉降量随着扩孔器钻进速度的增大呈现出上升趋势;在旋转速度上，单位位移上的沉降量会随着扩孔器旋转速度的增大而减小。在两条曲线的交点处，可以作为施工中扩孔器扩孔时的速度控制的理论参考值，有利于控制孔眼形状。

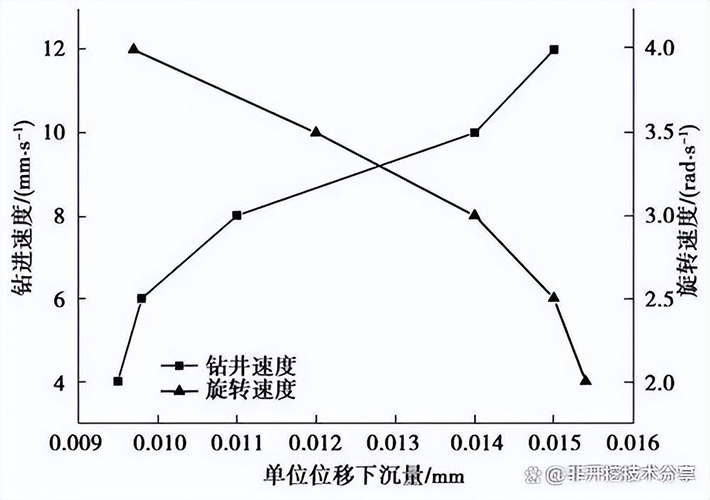
图 11 单位位移下扩孔器的下沉量

4.结论

水平定向扩孔的孔形问题是工程中经常遇到的又是必须考虑的实际问题。通过有限元数值模拟软件模拟了扩孔过程，得出1*3+1+19-10=29+73了如下结论:

(1) 通过单齿正交切削岩土的解析解验证了有限元模型的可靠性，充分说明了在求解地层岩土失效与岩土去除等高度非线性问题上，有限元方法具有一定的优势。

(2) 在扩孔器扩孔的过程中，除扩孔器的自重外，扩孔器的钻进速度和旋转速度对孔形的下沉量有显著的影响。扩孔过程中，扩孔器的下沉量会随着其钻进速度的增大而增大，但随着扩孔器旋转速度的增大，下沉量反而会减小。

(3) 在扩孔器钻进的单位位移上，下沉量会随着钻进速度的增加呈现上升趋势，下沉量会随着扩孔器自转速度的增加呈下降趋势，在上升趋势与下降趋势的交点处，可作为扩孔器运动参数的zui优理论值。